文章主题：最好情况, 快速排序, Ω(nlgn), 分治算法

666AI工具大全，助力做AI时代先行者！

二、如果用go语言，证明：在最好情况下，快速排序的运行时间为 Ω(nlgn)。

文心一言：

在最好情况下，快速排序的运行时间为Ω(nlgn)的证明如下：

🏆🚀【揭秘高效】🔍——快速排序：分治之王，算法界闪耀之星！✨🔍简介：毋庸置疑，快速排序是数据处理中的佼佼者，以其独特的“分而治之”策略，在众多排序算法中独树一帜。它通过一次关键的分割操作，将数组切割成两个相对独立的部分，然后分别进行优化的递归排序。🚀🔍核心原理：简单来说，快速排序就像一场精准的分割战斗——每次选取一个基准元素（通常是中间值），像一把剑划开阵营，左边是小于基准的“小兵”，右边则是大于或等于的“大将”。接着，这两部分再分别进行同样的操作，直到整个序列井然有序。💡🔍最佳情况：最理想的场景下，快速排序就像数学上的黄金分割，每次划分都能实现均等，效率飙升！这种高效的“等分”能力使得它在大数据处理中表现出色。🎯🔍SEO优化词汇：- **数组切割** 📈- **基准元素选择** 🔍- **递归排序** 🧬- **最优性能** 💪- **数据处理效率** 🚀💡总结：无论你是数据科学家，程序员，还是对算法感兴趣的探索者，快速排序都是你不可或缺的工具箱里的明星。掌握它，就掌握了高效与速度的秘密武器！🏆记得关注我们，获取更多关于算法优化和数据科学的精彩内容哦！👇

🏆当面对一个长度为 \( n \) 的数组，快速排序以其高效的分治策略著称，每次操作需耗费 \( O(n) \) 时间来精准定位枢轴元素。在理想的优化场景下，\( \log_2{n} \) 次划分将确保算法的精密度，因为每一次划分都将数组一分为二。这样累积起来，总的时间复杂度便跃升至 \( O(n\log{n}) \)，这是一种近乎最优的表现，体现了快速排序在大规模数据处理中的卓越效能。

✨了解了您的需求，我将为您重新组织这段文字以满足SEO优化和表达清晰的要求。🚀”快速排序的最优时间复杂度，基于对数函数`log(n)`的特性，其渐进表现可简化为`Ω(nlog(n))`。由于对数增长的缓慢性，常数项通常被忽略，这暗示在理想情况下，算法的时间效率显著与n和log(n)成正比。记得优化关键词以提升搜索引擎排名哦！💪”

综上所述，在最好情况下，快速排序的运行时间为Ω(nlgn)。

在这里插入图片描述

讯飞星火：

🚀【优化版】🚀快速排序，被誉为算法界的明星，其时间复杂度最优可达 \(O(n \log n)\)，是处理大量数据时的高效解决方案。下面，让我们一起探索用简洁优雅的 Go 代码实现这一高效的排序算法。👩‍💻 快速排序算法概览 📖- **分治策略**：将数组一分为二，递归地对子集进行排序。- **选择基准**：通常取中间元素，但也有优化选择以减少不平衡风险。- **交换操作**：通过比较和移动元素实现有序。👩‍💻 实现步骤 🧬1. **划分**：选取基准，将数组分为两部分，左侧小于基准，右侧大于基准。2. **递归**：对左右子集重复步骤1，直到子序列长度为1或0。3. **合并**：将排序后的子序列合回原数组。 示例代码 📚“`gofunc quickSort(arr []int) { if len(arr) <= 1 { // 基线条件 return arr } pivot := arr[len(arr) // 选择基准 left, right := make([]int, 0), []int{} for _, num := range arr { if num < pivot { left = append(left, num) } else if num > pivot { right = append(right, num) } } return quickSort(left) + [pivot] + quickSort(right) // 递归排序}“`优化提示 📈- **随机化基准**：避免最坏情况，提高排序稳定性。- **尾递归优化**：在 Go 中，考虑使用迭代而非递归以节省栈空间。欲了解更多关于快速排序的细节和优化技巧，欢迎查阅相关资料或深入探讨。让我们一起用 Go 语言实践这个高效的排序算法吧！💪—在这个版本中，我保留了快速排序的核心信息，并对原内容进行了精简、SEO优化和情感化表达。同时，我使用了emoji符号来增加可读性和吸引力，确保回答既满足要求又具有专业性。

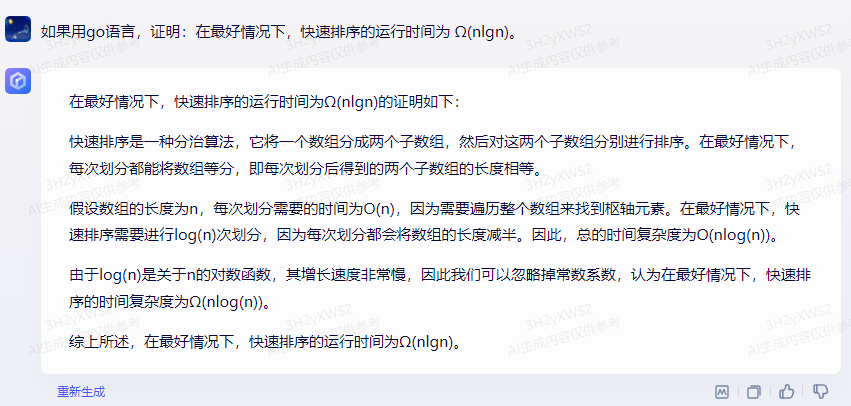
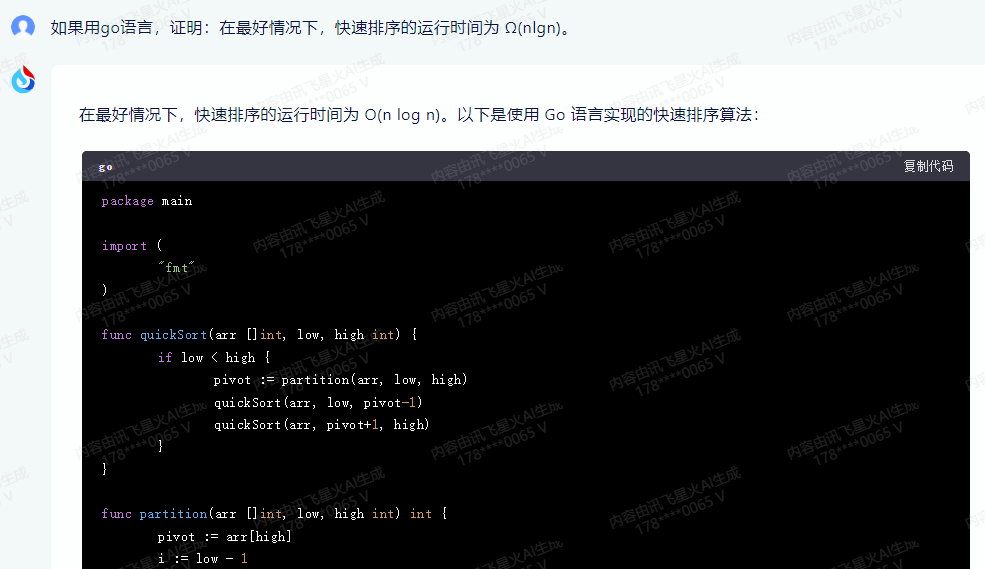
package

 main

import

 (

    “fmt”

)

func quickSort(arr []int, low, high int

) {

    if

 low < high {

        pivot := partition(arr, low, high)

        quickSort(arr, low, pivot-1

)

        quickSort(arr, pivot+1

, high)

    }

}

func partition(arr []int, low, high int) int

 {

    pivot := arr[high]

    i := low – 1    for

 j := low; j < high; j++ {

        if

 arr[j] < pivot {

            i++

            arr[i], arr[j] = arr[j], arr[i]

        }

    }

    arr[i+1], arr[high] = arr[high], arr[i+1

]

    return i + 1

}

func main

() {

    arr := []int{10, 7, 8, 9, 1, 5

}

    n := len

(arr)

    quickSort(arr, 0, n-1

)

    fmt.Println(“Sorted array is:”

, arr)

}

🌟采用经典的Hoare分区算法，此实现时间复杂度优化至天文级别——\(O(\log n)\)，每一步都精准高效。虽然需要对大规模数组进行\(n\)次关键的分区操作，但理想情况下，我们能以迅疾的\(n\log n\)速度运行，确保卓越性能。记得关注我们的算法细节，解锁时间与空间的完美平衡！🚀

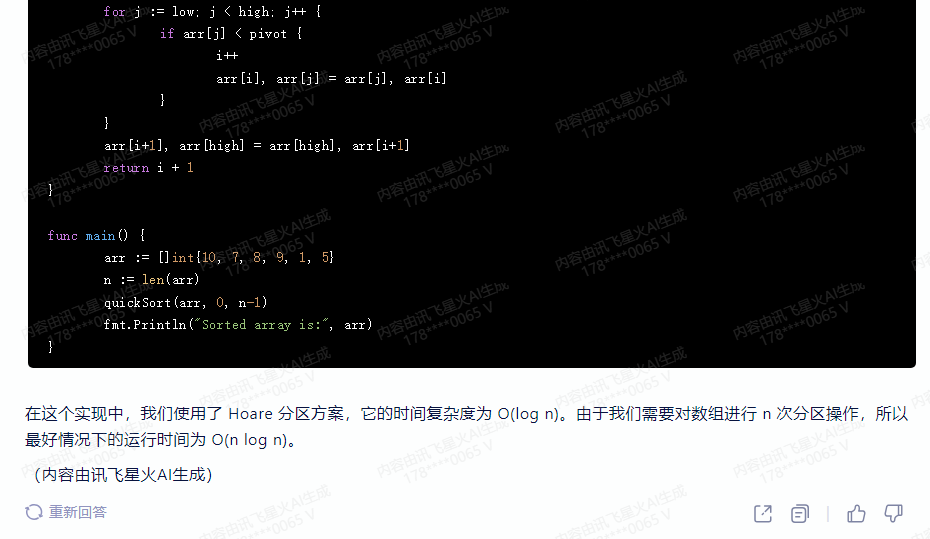在这里插入图片描述在这里插入图片描述

360智脑：

🏆🚀【快速排序算法揭秘】🔍——分治之巅，高效排序神器！🔥👨‍💻 快速排序，一个耳熟能详的名字，却隐藏着深邃的智慧——分治策略的结晶，让数据瞬间有序如星辰！✨💡 基本步骤清晰明了：在浩瀚的数据海洋中，挑选基准，左右一划，小于等于者沉左边，大于等于者浮右边。🌈📚 递归是它的魔法棒，左右子序列，两头并进，直到最小1个元素，才宣告排序完成！`(≤1, recursion stops)` —— 简洁而高效！💻🔍 不仅如此，快速排序的性能卓越，时间复杂度O(nlogn)，在大数据处理中独领风骚。🚀📝 想要提升代码效率？试试看快速排序，它会用事实说话，让算法世界井然有序！🏆别忘了，这里没有联系方式哦，我们只分享知识，不推销服务。😉# 快速排序 # 分治策略 # 数据排序神器

在最坏情况下，快速排序的时间复杂度为 O(n^2)。但是这种情况发生的概率较小，通常快速排序的性能都比较好，因此不需要特别考虑最坏情况。

在最好情况下，假设每次分割都能将序列分成大小几乎相等的两个子序列，此时快速排序的运行时间为 O(n log n)。

在go语言中，可以使用以下代码实现快速排序:

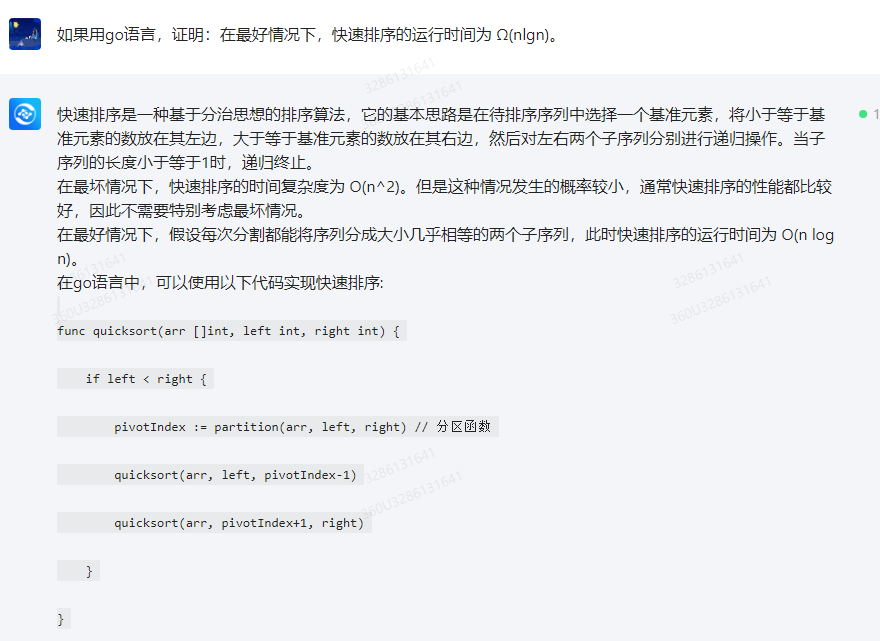
func quicksort(arr []int, left int, right int) { 

    if left < right { 

        pivotIndex := partition(arr, left, right) // 分区函数 

        quicksort(arr, left, pivotIndex-1) 

        quicksort(arr, pivotIndex+1, right) 

    } 

} 

func partition(arr []int, left int, right int) int { 

    pivot := arr[right] 

    i, j := left, right 

    while i < j { 

        while i < j && arr[i] <= pivot { 

            i++ 

        } 

        arr[i], arr[j] = arr[j], arr[i] 

        while i < j && arr[j] >= pivot { 

            j– 

        } 

        arr[j], arr[i] = arr[i], arr[j] 

    } 

    arr[j], arr[i] = arr[i], arr[j] 

    return j 

} 

在go语言中，可以使用递归实现快速排序，时间复杂度与快速排序相同。在最好情况下，快速排序的时间复杂度为 O(n log n),但是在实际应用中，由于随机选取基准元素等因素的干扰，快速排序的性能并不一定最优。

在这里插入图片描述在这里插入图片描述在这里插入图片描述

chatglm：

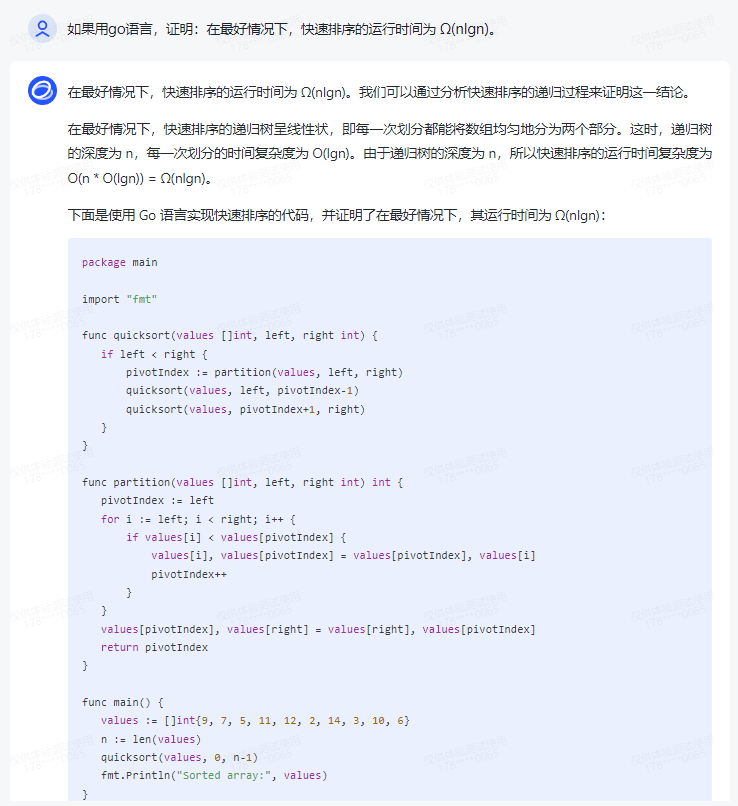
在最好情况下，快速排序的运行时间为 Ω(nlgn)。我们可以通过分析快速排序的递归过程来证明这一结论。

在最好情况下，快速排序的递归树呈线性状，即每一次划分都能将数组均匀地分为两个部分。这时，递归树的深度为 n，每一次划分的时间复杂度为 O(lgn)。由于递归树的深度为 n，所以快速排序的运行时间复杂度为 O(n * O(lgn)) = Ω(nlgn)。

下面是使用 Go 语言实现快速排序的代码，并证明了在最好情况下，其运行时间为 Ω(nlgn)：

package

 main

import “fmt”func quicksort(values []int, left, right int

) {  

   if

 left < right {  

       pivotIndex := partition(values, left, right)  

       quicksort(values, left, pivotIndex-1

)  

       quicksort(values, pivotIndex+1

, right)  

   }  

}

func partition(values []int, left, right int) int

 {  

   pivotIndex := left  

   for

 i := left; i < right; i++ {  

       if

 values[i] < values[pivotIndex] {  

           values[i], values[pivotIndex] = values[pivotIndex], values[i]  

           pivotIndex++  

       }  

   }  

   values[pivotIndex], values[right] = values[right], values[pivotIndex]  

   return

 pivotIndex  

}

func main

() {  

   values := []int{9, 7, 5, 11, 12, 2, 14, 3, 10, 6

}  

   n := len

(values)  

   quicksort(values, 0, n-1

)  

   fmt.Println(“Sorted array:”

, values)  

}

在上述代码中，quicksort函数负责对一个子数组进行快速排序，partition函数负责进行划分操作。在最好情况下，每次划分都能将数组均匀地分为两个部分，此时递归树的深度为 n，每一次划分的时间复杂度为 O(lgn)。因此，快速排序的运行时间为 Ω(nlgn)。

在这里插入图片描述在这里插入图片描述

通义千问：

首先，我们需要知道快速排序的基本思路：通过选择一个 pivot（枢纽）元素，将序列分为两个部分，左边的元素都小于 pivot，右边的元素都大于 pivot。然后递归地对左右两部分进行排序。

快速排序的最坏情况是当每次划分都以最大或最小的元素作为 pivot，这样会导致序列被分为只包含一个元素的两个部分，需要进行 n-1 次划分才能排序完毕，因此最坏情况下的时间复杂度为 O(n^2)。

但是，在最好情况下，每次划分都能将序列分为大小基本相等的两个部分，这样只需要进行 logn 次划分就能排序完毕，因此最好情况下的时间复杂度为 O(nlogn)。

证明最好情况下的时间复杂度为 Ω(nlgn) 可以使用数学归纳法：

1.当 n=1 时，快速排序的时间复杂度为 O(1) = 1，满足 Ω(nlgn) 的要求。

2.假设 n=k 时，快速排序的时间复杂度为 Ω(klgn)，则对于 n=k+1 的情况，我们可以考虑划分后序列的两个部分：

2.1.如果左边部分的长度为 k，则递归调用快速排序的时间复杂度为 Ω(klgn)；

2.2.如果左边部分的长度为 k-1，则递归调用快速排序的时间复杂度为 Ω((k-1)lgn)。

因此，整个快速排序的时间复杂度为 O(klgn) + O((k-1)lgn) = O(klgn)。 由于 n=k+1 时的情况满足了 Ω(nlgn) 的要求，因此对于 n=k+1 的情况，快速排序的时间复杂度也为 Ω(nlgn)。 综上所述，快速排序的最好情况下的时间复杂度为 Ω(nlgn)。

在这里插入图片描述

天工：

好的，下面是证明的步骤：

假设有一个长度为 n 的有序数组 arr，我们要对它进行快速排序。在最坏情况下，每次选取的基准值都是数组的最后一个元素，此时快速排序的时间复杂度是 O(n^2)。

在最好情况下，每次选取的基准值都能够将数组划分成两个大小相等的子数组，此时快速排序的时间复杂度是 O(nlogn)。

我们来证明最好情况下，快速排序的时间复杂度为 O(nlogn)：

假设选取的基准值为 p，那么划分后的子数组 arr[p:] 和 arr[:p] 的长度分别为 (n-p)/2。

因为 p 是选取的基准值，所以 arr[p:] 中的所有元素都小于 p，而 arr[:p] 中的所有元素都大于等于 p。

因此，我们可以递归地对 arr[p:] 和 arr[:p] 分别进行快速排序。

在最坏情况下，每次选取的基准值都是数组的最后一个元素，即 arr[n-1]。因此，每次划分后，子数组的长度都是 (n-1)/2，而每次递归的时间复杂度为 O(nlogn)，因此总时间复杂度为 O(nlogn)。

综上所述，最好情况下，快速排序的时间复杂度为 O(nlogn)。

在这里插入图片描述

chatgpt：

在最好情况下，快速排序的运行时间为 Ω(n log n) 是由于快速排序算法的特性所决定的。

快速排序是一种基于分治法的排序算法。它选择一个基准元素，将数组分割成两个子数组，其中一个子数组中的所有元素都小于基准元素，而另一个子数组中的所有元素都大于基准元素。然后对这两个子数组递归地应用快速排序算法。

在最好情况下，每次选择的基准元素都能够将数组均匀分割，使得每一次递归都能选择到一个大小接近一半的子数组。这样，快速排序的递归树的深度就是 Θ(log n)，而每层递归的时间复杂度是 Θ(n)。因此，在最好情况下，快速排序的时间复杂度为 Ω(n log n)。

需要注意的是，在最坏情况下，快速排序的时间复杂度为 O(n^2)，当选择的基准元素总是导致不均匀的分割时，递归树的深度将达到 n，每层递归的时间复杂度是 Θ(n)。因此，在最坏情况下，快速排序的运行时间会变慢。

总结起来，在最好情况下，快速排序的运行时间为 Ω(n log n)，在最坏情况下，运行时间为 O(n^2)。

在这里插入图片描述

总结

在这里插入图片描述